- Other Fluke companies:
- Fluke
- Fluke Biomedical
- Fluke Networks
- Fluke Process Instruments
Non-linear curve fitting using GNU plot
Metrology is a very satisfying occupation but there will be roadblocks along the way. For some of us curve fitting is easy so long as we have a standard software package that solves our problem. But what do you do in a situation where your usual software program doesn’t work because you’re dealing with a non-linear equation? Such situations are not that exotic. For example, infrared thermometers are everywhere and typically impractical to adjust. If you want to provide a correction table to your customer, then you’ll need to solve the Sakuma-Hattori equation.
There are a number of commercially available software packages that do an excellent job of performing non-linear curve fits. There are also commonly available software and public domain software that can also do this. Two of these are Microsoft Excel © and GNU Plot. Everybody likes getting something for free, so take a look at a couple examples of how to do a non-linear curve fit using these.
Fitting Target and Data
For this discussion, the Sakuma-Hattori equation in the Planckian Form (1) was considered as the fitting target. This equation is used in radiation thermometry to represent the response of a radiation thermometer to blackbody radiation over a range of blackbody temperatures. In Equation (1), A, B, and C are the parameters to be fitted; c2 is the Second Radiation Constant; T is the temperature in Kelvins; and S is the signal output of the radiation thermometer. A set of data that will be used to demonstrate these two methods is shown in Table 1. Both of the methods discussed here require initial guesses. For these examples, I made educated guesses based on experience.
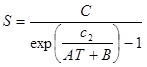 |
(1)
|
|
T / K
|
S / counts
|
U / K
|
|
258.16
|
44711
|
0.34
|
|
273.17
|
60235
|
0.30
|
|
323.23
|
133988
|
0.12
|
|
373.16
|
242965
|
0.11
|
|
473.15
|
563130
|
0.12
|
Fitting Using GNU Plot
There are several ways to do this fit using GNU Plot. I have found the one shown here to be the easiest. You will need to create two files: a script file and a data file. Both can be created using a simple text editor. The script file and the data file are shown in Figures 1 and 2 respectively. Figure 1 is configured to do a weighted curve fit. The function shown on the second line is the inverse of the Sakuma-Hattori Equation (1). The code to do a non-weighted curve fit is shown as well and is commented out. The text in Figure 2 can be separated by tabs or spaces.
|
# Blog Article Example
f(x) = c2 / A / log(C/x + 1) - B / A
c2 = 14387.752
A = 10
B = 100
C = 1e6
# weighted curve fit
fit f(x) 't_s.txt' using 2:1:3 via A, B, C
plot 't_s.txt' using 1:($f($$2) - $$1):3 title "" with yerrorbars
set title "SH Curve Fit - Weighted - Final"
replot
pause -1
# no weight curve fit
# fit f(x) 't_s.txt' using 2:1 via A, B, C
# plot 't_s.txt' using 1:($f($$2) - $$1) title ""
# set title "SH Curve Fit - Non Weighted - Final"
# replot
# pause -1
|
|
258.16 44711 0.34
273.17 60235 0.30
323.23 133988 0.12
373.16 242965 0.11
473.15 563130 0.12
|
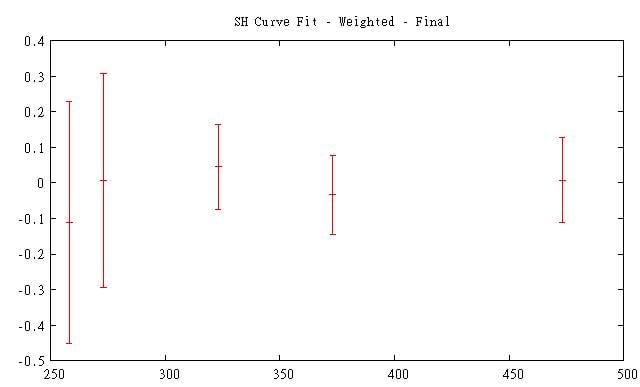
To do the curve fit, simply run GNU Plot, change to your local directory, and use the call function followed by the script file name in quotes. The fitted parameters will be outputted in a text window. The example in Figure 1 plots a graph of the fitting error and is shown in Figure 3.
Using Microsoft Excel
Using Excel, one may write a VBA macro to perform a curve fit. That is not a simple task. Microsoft provides an easier solution in the form of an add-in to Excel called Solver. It is not installed with a standard Excel installation, but a web search for “Solver Excel Install Add in” should give instructions for your specific version of Excel. (Note: we are not discussing ‘Open Solver’ here).
My initial data is shown in Table 2. The parameters are listed on top. Columns 1, 2, and 3 contain the reference temperature, the signal, and the expanded uncertainty of temperature (k = 2). Column 4 contains the result with the given parameters calculated using the inverse of the Sakuma-Hattori Equation (1). Column 5 contains the curve fit error divided by the uncertainty. This is done for a weighted curve fit. If the curve fit were not weighted, we would not divide by the uncertainty. Column 6 is Column 5 squared. Finally, we sum all of the squares of errors which is shown above Column 6. This is what we are trying to minimize. The chi squared result is shown above. Since we are using expanded uncertainties (k = 2), it is the sum of the errors squared multiplied by 4 (2 squared). This would not be the case for a non-weighted curve fit.
|
A
|
10
|
||||
|
B
|
100
|
||||
|
C
|
1000000
|
chi^2
|
3.56E+8
|
||
|
c2
|
14387.75
|
sum(e^2)
|
88966085
|
||
|
T / K
|
S / counts
|
U / K
|
CF / K
|
error / U
|
(e/U)^2
|
|
258.16
|
44711
|
0.34
|
446.57
|
554.14
|
307076
|
|
273.17
|
60235
|
0.30
|
491.67
|
728.32
|
530451.7
|
|
323.23
|
133988
|
0.12
|
663.66
|
2836.95
|
8048291
|
|
373.16
|
242965
|
0.11
|
871.42
|
4529.64
|
20517618
|
|
473.15
|
563130
|
0.12
|
1399.27
|
7717.68
|
59562649
|
For my version of Excel, I followed these steps to perform the curve fit. I opened Solver. I placed the sum of error squared into the ‘Set Objective’ box. I picked the ‘To: Min’ radio button. Then under ‘By Changing Variable Cells’, I picked the cells with parameters A, B, and C. Do not pick c2, as it is a physical constant. Under ‘Select a Solving Method’, I picked ‘GRG-Nonlinear’. Under Options -> GRG-Nonlinear, I used 0.000000000001 for convergence. Then I clicked ‘Solve’.
Comparison of Answers
Both Excel and GNU Plot gave the same answers. Table 3 shows the results. The real differentiation between the two software packages is which is more convenient for your own use. GNU Plot is free. However, it is cumbersome to use. Microsoft Excel is not free, but in the modern day work place, most people have it installed on their computer.
|
Parameter
|
GNU Plot
|
Excel
|
|
A
|
9.27358
|
9.27358
|
|
B
|
145.503
|
145.503
|
|
C
|
1.28939e7
|
1.28939e7
|
|
χ2
|
1.4043
|
1.4043
|
Links
- Login or register to post comments
- Printer-friendly version »
- Home
- Products
- New Products
- Electrical Calibration
- RF Calibration
- Data Acquisition and Test Equipment
- Temperature Calibration
- Humidity Calibration
- Pressure Calibration
- Flow Calibration
- Process Calibration Tools
- Calibration Software
- Service and Support
- All Calibration Instruments
- Handheld Test Tools
- Purchase Info
- News
- Training and Events
- Literature and Education
- Service and Support
- About Us


